Bradley Math Problem-Solving Group

The Schedule

We meet once or twice a week to talk about math problems and how to solve them.

Our next meeting is Thursday, 5 March at 4 p.m. in Bradley 451.

Don't forget that the ISMAA Competition is coming up March 30th.

The Participants

Everyone is invited.

So far this year, the following people have attended meetings:
Andrew Durre, Brian Biggs, Danielle Harnack, Michael Lang, Morgan Crawford, Paul Bruno, Rachel Thurwanger, Robert Andry, and Robert Miller.

Paul entered the Putnam competition December 2nd, as did Rob Andry.

The Facts and Techniques

These are useful ideas and suggestions we've reminded ourselves of.

The Problems

If you have a problem to add to the list, feel free to suggest it.

Problem Posed Solved Hint
Nonlinear Recurrence 29 Mar

Triangle Inequality 12 Mar 26 Mar
 Use the arithmetic-geometric mean inequality.
Square Angle 12 Mar 12 Mar
 Move things around.
Number of Digits 12 Mar 12 Mar
 How many digits does A have?
Integral 12 Mar 12 Mar
 Create and use some symmetry.
Circle Regions 1 Mar 8 Mar
 Use the Euler characteristic.
Region Crossings 22 Feb 1 Mar
 How many times can your line or circle cross the boundary lines?
Parallelogram Triangles 19 Feb 19 Feb
 Add some more triangles.
Finite Solutions 19 Feb 19 Feb
 Make the problem more general -- it's true for any RHS.
Possible Length 19 Feb 19 Feb
 Make some right triangles.
Integral Limit 19 Feb 19 Feb
 Use FTC.
Cyclic Reciprocal Inequality 15 Feb 15 Feb
 Use the arithmetic-geometric mean inequality.
Dice Faces 8 Feb 8 Feb
 What is the sum of opposite faces of a die?
Association 16 Nov 8 Feb
 Remember that a and b can be anything in the set.
Closed Subset 14 Nov 16 Nov
 Prove by contradiction.
Hemisphere 17 Oct 13 Nov
 How many points can you force onto the edge of a hemisphere?
Square Sum 19 Sep 16 Oct
 Use either Lagrange or Cauchy-Schwarz.
Intersection Average 15 Sep 18 Sep
 Focus on the cubic term.
Double Integer 12 Sep 14 Sep
 Isolate the first digit.
Sum Product 11 Sep 11 Sep
 Try Cauchy-Schwarz.
Unit Fractions 5 Sep 11 Sep
 How can you resolve repetition?
Integer Solutions 4 Sep 14 Sep
 Think about parity.
7x7 Knights 1 Sep 4 Sep
 Color the board.

Nonlinear Recurrence

Consider an integer sequence whose ith term is twice the sum of the digits of the (i-1)st term. Prove that if the first term is a power of two then the sequence contains a one-digit number. Prove that if the first term is a power of three (bigger than 9) then the sequence doesn't contain a one-digit number.

Triangle Inequality

Let a, b and c be the lengths of the sides of a triangle. Show that (a+b-c)(a-b+c)(-a+b+c) is no bigger than abc.

Square Angle

Let ABCD be a square and let n be a natural number. Let X1, X2, ..., Xn be points on BC such that BX1=X1X2=...=XnC. Let Y be a point on AD such that AY=BX1. Find the sum of the measures of the angles AX1Y, AX2Y, ..., AXnY and ACY.

Number of Digits

Suppose that A is a natural number and B=A3. Is it possible that the number of digits in A plus the number of digits in B equals 2001?

Integral

Evaluate .

Circle Regions

If you pick n points on a circle and connect each pair by a straight line, what is the maximum number of regions created?

Region Crossings

2001 lines are drawn in the plane, creating many regions. How many of these regions can another line intersect? How many of these regions can a circle intersect?

Parallelogram Triangles

Suppose ABCD is a parallelogram, M is the midpoint of AB, and P is the intersection of MD and AC. Find the ratio of the area of triangle AMP to the area of parallelogram ABCD.

Finite Solutions

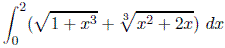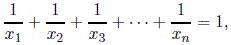Let n be a natural number. Prove that there are finitely many solutions to the equation where the x's are all natural numbers.

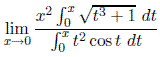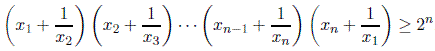Possible Length

Suppose that ABCD is a rectangle and E is a point inside ABCD with AE = 1, CE = 2 and DE = 3. Find all possible lengths for BE.

Integral Limit

Evaluate .

Cyclical Reciprocal Inequality

Given x1,...,xn, all positive reals, prove .

Dice Faces

You roll 2000 dice one time and find that the ratio of the sum of the numbers on the top faces to the sum of the numbers of the bottom was again an integer. How many different integers are possible for the sum of the numbers on the top faces?

Association

Consider a set S and a binary operation * such that for every a and b in S, a*b is in S. Assume that (a*b)*a=b for all a and b in S. Prove that a*(b*a)=b for all a and b in S.

Closed Subset

Let S be a set of real numbers which is closed under multiplication (that is, if a and b are in S, then so is ab). Let T and U be disjoint subsets of S whose union is S. Given that the product of any three (not necessarily distinct) elements of T is in T and that the product of any three elements of U is in U, show that at least one of the two subsets T,U is closed under multiplication.

Hemisphere

Given any five points on a sphere, show that some four of them must lie on a closed hemisphere.

Square Sum

Suppose that the sum of n real numbers is one. Show that the sum of the squares of these numbers is at least 1/n.

Intersection Average

Let f(x) be some fourth-degree polynomial. Consider any line that meets the graph of y=f(x) in four distinct points. Does the average of the x-coordinates of these points depend on your choice of line?

Double Integer

Does there exist a positive integer that is doubled when the initial digit is moved to the end?

Sum Product

Show (a1+a2+...+an)(1/a1+1/a2+...+1/an)>=n2.

Unit Fractions

A "unit fraction" is a fraction with 1 for its numerator. Can every positive rational number be written as the sum of distinct unit fractions?

Integer Solutions

Find all positive integer solutions to a2+b2+c2+d2=2n.

7x7 Knights

Consider a 7x7 "chessboard" with a knight on each square.
Is it possible for all of the knights to move, simultaneously and legally, so that no two land on the same square?
This page is maintained by Michael Lang.